 Waves in the environment
Waves in the environmentBy Dr J Floor Anthoni
Without waves, the world would be a different place. Waves cannot exist by themselves for they are caused by winds. Winds in turn are caused by differences in temperature on the planet, mainly between the hot tropics and the cold poles but also due to temperature fluctuations of continents relative to the sea.
Without waves, the winds would have only a very small grip on the water and would not be able to move it as much. The waves allow the wind to transfer its energy to the water's surface and to make it move. At the surface, waves promote the exchange of gases: carbon dioxide into the oceans and oxygen out. Currents and eddies mix the layers of water which would otherwise become stagnant and less conducive to life. Nutrients are thus circulated and re-used. The large ocean currents transport warm water from the tropics to the poles and cold water the other way. They help to stabilise the planet's temperature and to minimise its extremes. For instance, because of warm ocean currents arriving from the north, the temperature of New Zealand is 3-4 degrees higher than it would be without them.
For the creatures in the sea, ocean currents allow their larvae to be dispersed and to be carried great distances. Many creatures spawn only during storms when large waves can mix their gametes effectively.
Coastal creatures living in shallow water experience the brunt of the waves directly. In order to survive there, they need to be robust and adaptable. Thus waves maintain a gradient of biodiversity all the way from the surface, down to depths of 30m or more. Without waves, there would not be as many species living in the sea.
Waves pound rocks and make them erode faster, but sea organisms covering these rocks, delay this process. Waves make beaches by transporting sand from deeper down towards the shore and by washing the sand and removing fine particles. Waves stir and suspend the sand so that currents or gravity can transport it.
Wave motion
Anyone having watched water waves rippling outward from the point where a stone was thrown in, should have noticed how effortlessly waves can propagate along the water's surface. Wherever we see water, we see its surface stirred by waves. Indeed, witnessing a lake or sea flat like a mirror, is rather unusual. Yet, as familiar we are with waves, we are unfamiliar with how water particles can join forces to make such waves.
Waves are oscillations in the water's surface. For oscillations to exist and to propagate, like the vibrating of a guitar string or the standing waves in a flute, there must be a returning force that brings equilibrium. The tension in a string and the pressure of the air are such forces. Without these, neither the string nor the flute could produce tones. The standing waves in musical instruments bounce their energy back and forth inside the string or the flute's cavity. The oscillations that are passed to the air are different in that they travel in widening spheres outward. These travelling waves have a direction and speed in addition to their tone or timbre. In air their returning force is the compression of the air molecules. In surface waves, the returning force is gravity, the pull of the Earth. Hence the name 'gravity waves' for water waves.
In solids, the molecules are tightly connected together, which prevents them from moving freely, but they can vibrate. Water is a liquid and its molecules are allowed to move freely although they are placed closely together. In gases, the molecules are surrounded by vast expanses of vacuum space, which allows them to move freely and at high speed. In all these media, waves are propagated by compression of the medium. However, the surface waves between two media (water and air), behave very different and solely under the influence of gravity, which is much weaker than that of elastic compression, the method by which sound propagates.
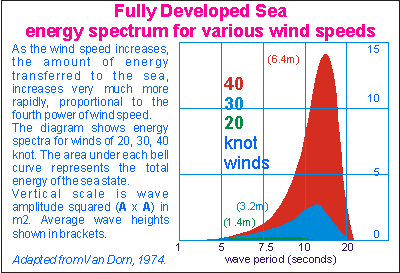
If each water particle makes small oscillations around its spot, relative to its neighbours, waves can form if all water particles move at the same time and in directions that add up to the wave's shape and direction. Because water has a vast number of molecules, the height of waves is theoretically unlimited. In practice, surface waves can be sustained as high as 70% of the water's depth or some 3000m in a 4000m deep sea (Van Dorn, 1974).
Note that the water particles do not travel but only their collective energy does! Waves that travel far and fast, undulate slowly, requiring the water particles to make slow oscillations, which reduces friction and loss of energy.
Water waves can store or dissipate much energy. Like other waves (alternating electric currents, e.g.), a wave's energy is proportional to the square of its height (potential). Thus a 3m high wave has 3x3=9 times more energy than a 1m high wave. When fine-weather waves of about 1m height pound on the beach, they dissipate an average of 10kW (ten one-bar heaters) per metre of beach or the power of a small car at full throttle, every five metres. (Ref Douglas L Inman in Oceanography, the last frontier, 1974). Attempts to harness the energy from waves have failed because they require large structures over large areas and these structures should be capable of surviving storm conditions with energies hundreds of times larger than they were designed to capture.
Waves have a direction and speed. Sound waves propagate by compressing the medium. They can travel in water about 4.5 times faster than in air, about 1500m per second (5400km/s, or mach-4.5, depending on temperature and salinity). Such waves can travel in all directions and reach the bottom of the ocean (about 4km) in less than a second. Surface waves, however, are limited by the density of water and the pull of gravity. They can travel only along the surface and their wave lengths can at most be about twice the average depth of the ocean (2 x 4 km). The fastest surface waves observed, are those caused by tsunamis. The 'tidal wave' caused by an under-sea earthquake in Chile in May 1960, covered the 6000 nautical miles (11,000km) to New Zealand in about 12 hours, travelling at a speed of about 900 km/hr! When it arrived, it caused an oscillation in water level of 0.6m at various places along the coast, 1.4m in Tauranga Harbour and 2.4m in Whitianga harbour. Note that tsunamis reach their minimum at about 6000 km distance. Beyond that, the curvature of the Earth bends the wave fronts to focus them again at a distance of about 12,000 km, where they can still cause considerable damage.
The rougher the water becomes, the easier it is for the wind to transfer its energy. The waves become steep and choppy. Further away from the shore, the water's surface is not only stirred by the wind but also by waves arriving with the wind. These waves influence the motion of the water particles such that opposing movements gradually cancel out, whereas synchronising movements are enhanced. The waves start to become more rounded and harmonious. Depending on duration and distance (fetch), the waves develop into a fully developed sea.
Anyone familiar with the sea, knows that waves never assume a uniform, harmonious shape. Even when the wind has blown strictly from one direction only, the resulting water movement is made up of various waves, each with a different speed and height. Although some waves are small, most waves have a certain height and sometimes a wave occurs which is much higher.
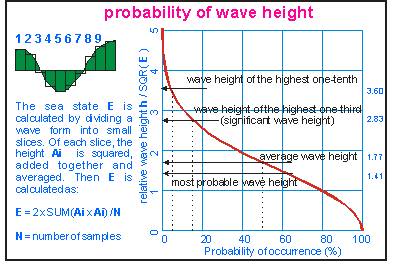 When trying to be more precise about waves, difficulties arise: how do we measure waves objectively? When is a wave a wave and should be counted? Scientists do this by introducing a value E which is derived from the energy component of the compound wave. In the left part of the drawing is shown how the value E is derived entirely mathematically from the shape of the wave. Instruments can also measure it precisely and objectively. The wave height is now proportional to the square root of E. When trying to be more precise about waves, difficulties arise: how do we measure waves objectively? When is a wave a wave and should be counted? Scientists do this by introducing a value E which is derived from the energy component of the compound wave. In the left part of the drawing is shown how the value E is derived entirely mathematically from the shape of the wave. Instruments can also measure it precisely and objectively. The wave height is now proportional to the square root of E. The sea state E is two times the average of the sum of the squared amplitudes of all wave samples.The right part of the diagram illustrates the probability of waves exceeding a certain height. The vertical axis gives height relative to the square root of the average energy state of the sea: h / SQR( E ) . For understanding the graph, one can take the average wave height at 50% probability as reference. Fifty percent of all waves exceed the average wave height, and an equal number are smaller. The highest one-tenth of all waves are twice as high as the average wave height (and four times more powerful). Towards the left, the probability curve keeps rising off the scale: one in 5000 waves is three times higher and so on. The significant wave height H3 is twice the most probable height and occurs about 15% or once in seven waves, hence the saying "Every seventh wave is highest". Click here for a larger version of this diagram. |
For the complete series visit: Seafriends.org
Weather Story;
Typhoon Usagi is tracking closer to Japan and expect to hit the island today. To top that one, a small tsunami hit the Japanese Island of Hokkaido, no damage was reported. Tropical Storm Eric is still spinning in he eastern pacific and TS Chantel is off the NHC radar.
RS
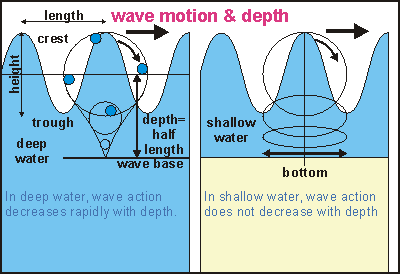 In the diagram some familiar terms are shown. A floating object is observed to move in perfect circles when waves oscillate harmoniously sinus-like in deep water. If that object hovered in the water, like a water particle, it would be moving along diminishing circles, when placed deeper in the water. At a certain depth, the object would stand still. This is the wave's base, precisely half the wave's length. Thus long waves (ocean swell) extend much deeper down than short waves (chop). Waves with 100 metres between crests are common and could just stir the bottom down to a depth of 50m. Note that the depth of a wave has little to do with its height! But a wave's height contains the wave's energy, which is unrelated to the wave's length. Long surface waves travel faster and further than short ones. Note also that the forward movement of the water under a crest in shallow water is faster than the backward movement under its trough. By this difference, sand is swept forward towards the beach.
In the diagram some familiar terms are shown. A floating object is observed to move in perfect circles when waves oscillate harmoniously sinus-like in deep water. If that object hovered in the water, like a water particle, it would be moving along diminishing circles, when placed deeper in the water. At a certain depth, the object would stand still. This is the wave's base, precisely half the wave's length. Thus long waves (ocean swell) extend much deeper down than short waves (chop). Waves with 100 metres between crests are common and could just stir the bottom down to a depth of 50m. Note that the depth of a wave has little to do with its height! But a wave's height contains the wave's energy, which is unrelated to the wave's length. Long surface waves travel faster and further than short ones. Note also that the forward movement of the water under a crest in shallow water is faster than the backward movement under its trough. By this difference, sand is swept forward towards the beach.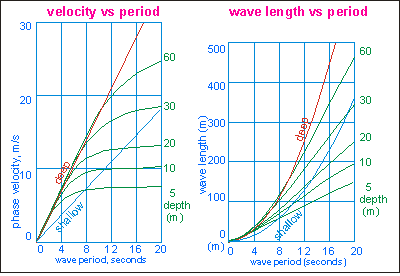
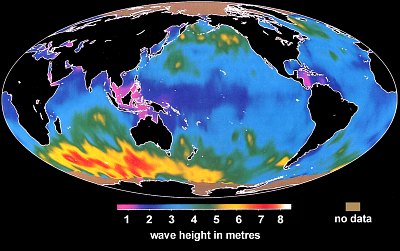 The biggest waves on the planet are found where strong winds consistently blow in a constant direction. Such a place is found south of the Indian Ocean, at latitudes of -40º to -60º, as shown by the yellow and red colours on this satellite map. Waves here average 7m, with the occasional waves twice that height! Directly south of New Zealand, wave heights exceeding 5m are also normal. The lowest waves occur where wind speeds are lowest, around the equator, particularly where the wind's fetch is limited by islands, indicated by the pink colour on this map. However, in these places, the sea water warms up, causing the birth of tropical cyclones, typhoons or hurricanes, which may send large waves in all directions, particularly in the direction they are travelling.
The biggest waves on the planet are found where strong winds consistently blow in a constant direction. Such a place is found south of the Indian Ocean, at latitudes of -40º to -60º, as shown by the yellow and red colours on this satellite map. Waves here average 7m, with the occasional waves twice that height! Directly south of New Zealand, wave heights exceeding 5m are also normal. The lowest waves occur where wind speeds are lowest, around the equator, particularly where the wind's fetch is limited by islands, indicated by the pink colour on this map. However, in these places, the sea water warms up, causing the birth of tropical cyclones, typhoons or hurricanes, which may send large waves in all directions, particularly in the direction they are travelling.































































































![Validate my RSS feed [Valid RSS]](valid-rss.png)